Quantum Machine Learning A New Frontier

Quantum machine learning is poised to revolutionize how we approach complex problems. By leveraging the principles of quantum mechanics, this emerging field promises to surpass the capabilities of classical machine learning, offering significant speedups and the potential to solve currently intractable problems. This exploration will delve into the fundamental concepts, algorithms, and applications of this exciting area, examining both its immense potential and the challenges that lie ahead.

We’ll examine how quantum computers, harnessing phenomena like superposition and entanglement, can process information in fundamentally different ways than classical computers. This difference allows for the development of novel algorithms that can tackle machine learning tasks with unprecedented efficiency. We’ll explore specific quantum algorithms, like Grover’s algorithm and quantum annealing, and discuss their impact on tasks such as classification, regression, and optimization.

The journey will also cover the intricacies of quantum data encoding, the architecture of quantum machine learning models, and the real-world applications currently under development.

Introduction to Quantum Machine Learning

Quantum machine learning (QML) is a rapidly developing field that combines the principles of quantum computing with machine learning algorithms. It promises to revolutionize how we approach complex computational problems by leveraging the unique properties of quantum mechanics. This introduction will explore the fundamental differences between classical and quantum computing, highlight the potential advantages of QML, and provide examples of real-world applications.Quantum computing harnesses the bizarre yet powerful phenomena of quantum mechanics, such as superposition and entanglement, to perform computations.

Unlike classical bits, which represent either 0 or 1, quantum bits (qubits) can exist in a superposition, representing both 0 and 1 simultaneously. This allows quantum computers to explore many possibilities concurrently, potentially leading to exponential speedups for certain types of problems. Entanglement, another key quantum phenomenon, links the fates of two or more qubits, regardless of the physical distance separating them.

This interconnectedness allows for highly efficient information processing. Classical computers, on the other hand, rely on deterministic bit manipulation, processing information sequentially.

Potential Advantages of Quantum Machine Learning

Quantum machine learning offers several potential advantages over classical machine learning. The ability of qubits to exist in superposition enables quantum algorithms to explore a vastly larger solution space simultaneously compared to classical algorithms. This can lead to significant improvements in the speed and efficiency of training machine learning models, particularly for complex problems where classical algorithms struggle.

Furthermore, quantum algorithms can potentially solve certain optimization problems that are intractable for classical computers, unlocking new possibilities in areas such as drug discovery and materials science. The enhanced parallelism inherent in quantum computing can also facilitate the handling of massive datasets that would overwhelm classical systems.

Real-World Applications of Quantum Machine Learning

Several real-world problems stand to benefit significantly from quantum machine learning solutions. One promising area is drug discovery and materials science. Quantum computers could simulate the behavior of molecules with unprecedented accuracy, accelerating the identification of new drugs and the design of novel materials with specific properties. Another area is financial modeling. QML algorithms could potentially improve the accuracy of risk assessment models and optimize investment portfolios.

Furthermore, quantum machine learning could revolutionize fields like artificial intelligence, leading to more efficient and powerful AI systems capable of tackling previously unsolvable problems. For instance, advancements in quantum algorithms could improve image recognition and natural language processing capabilities.

Comparison of Classical and Quantum Machine Learning Algorithms

The following table compares some classical and quantum machine learning algorithms, highlighting their key differences and potential advantages.

Algorithm Type	Algorithm Name	Description	Potential Advantages
Classical	Support Vector Machine (SVM)	A supervised learning model used for classification and regression.	Widely used, well-understood, efficient for smaller datasets.
Classical	Neural Network	A complex model inspired by the human brain, used for various tasks including image recognition and natural language processing.	High accuracy for complex tasks, adaptable to various problems.
Quantum	Quantum Support Vector Machine (QSVM)	A quantum version of SVM, potentially offering speedups for high-dimensional data.	Potential for faster training and improved accuracy compared to classical SVM for certain datasets.
Quantum	Variational Quantum Eigensolver (VQE)	Used for finding the lowest energy state of a quantum system, applicable to various machine learning tasks.	Potential for solving optimization problems intractable for classical computers.

Quantum Algorithms for Machine Learning

Quantum computing offers the potential to revolutionize machine learning by leveraging the principles of superposition and entanglement to solve problems intractable for classical computers. This section explores several key quantum algorithms and their applications within the machine learning landscape, comparing their performance against classical counterparts.

Grover’s Algorithm in Quantum Machine Learning

Grover’s algorithm is a quantum search algorithm that can quadratically speed up the search for a specific item within an unsorted database compared to classical algorithms. In machine learning, this translates to faster searches within large datasets. For instance, consider a scenario involving finding the optimal hyperparameters for a machine learning model. A classical approach might involve exhaustively testing numerous combinations.

Quantum machine learning holds incredible potential, offering faster and more efficient algorithms than classical methods. However, its development is intertwined with the broader implications of Quantum AI, especially concerning cybersecurity; check out this article on Quantum AI’s impact on cybersecurity and data encryption to see how it’s shaping the future. Understanding these security challenges is crucial for the responsible development and deployment of quantum machine learning applications.

Grover’s algorithm, however, can significantly reduce the search time, leading to quicker model training and optimization. The quadratic speedup, while impressive, is limited by the size of the search space; for extremely large datasets, the benefit might still be overshadowed by other computational bottlenecks.

Quantum Annealing in Machine Learning Optimization

Quantum annealing is a metaheuristic optimization algorithm that uses quantum fluctuations to find the global minimum of a cost function. This is particularly useful in machine learning for solving optimization problems such as feature selection, model parameter tuning, and training neural networks. In feature selection, for example, quantum annealing can efficiently identify the most relevant features from a high-dimensional dataset, improving model accuracy and reducing computational complexity.

The D-Wave quantum annealers are a prominent example of hardware implementing this approach, although their applicability is often context-dependent and requires careful consideration of problem formulation and the limitations of the hardware itself. A real-world example might involve optimizing the parameters of a recommendation system, where quantum annealing could significantly speed up the process of finding the optimal weights for personalized recommendations.

Comparison of Quantum and Classical Algorithms for Machine Learning Tasks

A direct comparison of quantum and classical algorithms for machine learning tasks often depends heavily on the specific task and the size of the dataset. For tasks like classification and regression, quantum algorithms like Quantum Support Vector Machines (QSVM) have shown potential for improved performance in specific scenarios, particularly when dealing with high-dimensional data or complex relationships. However, current quantum computers are still limited in their capabilities, and for many tasks, classical algorithms remain more efficient and readily available.

Furthermore, the overhead associated with encoding data and running algorithms on quantum hardware often outweighs the theoretical speedup for smaller datasets. A significant amount of research is still needed to fully realize the potential of quantum algorithms in practical machine learning applications. The development of more powerful and error-corrected quantum computers is crucial for a more comprehensive and decisive comparison.

Flowchart of a Quantum Support Vector Machine (QSVM) Algorithm

The following flowchart Artikels the steps involved in a simplified version of a QSVM algorithm. Note that this is a simplified representation and actual implementations can be significantly more complex.[Imagine a flowchart here. The flowchart would start with “Input Data,” leading to “Data Encoding (Quantum State Preparation),” then to “Quantum Kernel Computation,” followed by “Quantum Optimization (e.g., Grover’s algorithm for finding the optimal hyperplane),” and finally to “Output: Classification Result.”] The data encoding step involves transforming the classical data into a suitable quantum state.

The quantum kernel computation uses quantum algorithms to efficiently compute the kernel function, a crucial component of SVMs. The quantum optimization step leverages quantum algorithms to find the optimal hyperplane that separates the data points into different classes. The output is the classification result for new data points.

Quantum Machine Learning Models

Quantum machine learning leverages the principles of quantum mechanics to develop novel algorithms and models that can potentially surpass the capabilities of classical machine learning approaches in certain tasks. This section explores some key quantum machine learning models, highlighting their architectures and functionalities, and comparing their strengths and weaknesses.

Quantum Support Vector Machines (QSVMs)

Quantum Support Vector Machines aim to improve the efficiency and accuracy of classical SVMs by utilizing quantum computation. A classical SVM finds an optimal hyperplane that maximizes the margin between different classes of data points. A QSVMs, however, can potentially achieve this optimization more efficiently by leveraging quantum algorithms like quantum annealing or variational quantum eigensolvers. The architecture involves mapping the data points and their features into a higher-dimensional Hilbert space, where the optimal hyperplane is found using quantum algorithms.

This allows for the exploration of a much larger feature space than is computationally feasible with classical SVMs, potentially leading to better classification accuracy. The functionality revolves around optimizing a quantum cost function representing the margin maximization problem. Different QSVM implementations use different quantum algorithms for this optimization, leading to variations in their performance and scalability. For instance, a QSVM utilizing a quantum annealing approach might be more suited for smaller datasets with specific structures, while a variational quantum eigensolver-based QSVM could handle larger datasets but potentially require more resources.

Classical vs. Quantum Neural Networks

Classical neural networks rely on artificial neurons that process information using classical logic gates. Quantum neural networks, on the other hand, utilize quantum bits (qubits) and quantum gates to perform computations. Key differences include the nature of the processing units (classical bits vs. qubits), the type of operations performed (classical logic gates vs. quantum gates), and the potential for quantum phenomena like superposition and entanglement to enhance learning capabilities.

Classical neural networks are limited by the exponential growth of computational complexity with increasing network size and data dimensionality. Quantum neural networks, while still facing scalability challenges, have the theoretical potential to overcome some of these limitations by exploiting quantum parallelism. For example, a quantum neural network could potentially perform calculations on multiple data points simultaneously using superposition, leading to faster training and inference times compared to its classical counterpart.

However, building and training large-scale quantum neural networks is a significant technological challenge currently.

Quantum machine learning is a rapidly developing field exploring the potential of quantum computers to solve complex problems. A key area of this research involves leveraging advancements in Quantum AI to create more efficient and powerful machine learning algorithms. This ultimately aims to enhance the capabilities of quantum machine learning models, leading to breakthroughs in various sectors.

Examples of Quantum-Enhanced Clustering Algorithms

Quantum algorithms can potentially enhance classical clustering algorithms by offering speedups in specific aspects. One example involves using quantum annealing to find the optimal partitioning of data points into clusters. Quantum annealing can efficiently explore the vast landscape of possible cluster assignments, potentially finding better solutions than classical algorithms in reasonable time, particularly for high-dimensional data. Another approach involves using quantum algorithms to compute similarity measures between data points more efficiently.

For instance, quantum algorithms could be employed to calculate distances or kernels between data points faster, which would then be used as input to a classical clustering algorithm. These quantum enhancements can improve the overall efficiency and scalability of clustering algorithms, especially when dealing with large and complex datasets. The specific quantum algorithms used and their implementation would influence the degree of improvement achieved.

Comparison of Quantum Machine Learning Models

Model	Scalability	Accuracy (Potential)	Current Limitations
QSVMs	Limited by the size of the quantum computer and the complexity of the quantum algorithm used.	Potentially higher than classical SVMs due to exploration of higher-dimensional feature spaces.	Requires efficient quantum algorithms for optimization, availability of sufficiently large quantum computers.
Quantum Neural Networks	Highly limited by current quantum hardware capabilities; significant scalability challenges remain.	Theoretically capable of surpassing classical neural networks, but this potential is yet to be fully realized.	Hardware limitations, noise in quantum computations, development of efficient quantum training algorithms.
Quantum-Enhanced Clustering	Scalability depends on the specific quantum algorithm used; some approaches offer better scalability than others.	Accuracy can be improved over classical methods in certain cases, but it’s problem-dependent.	Requires efficient quantum algorithms for distance calculations or optimization, access to suitable quantum hardware.

Quantum Data Representation and Encoding

Encoding classical data for quantum algorithms requires translating classical information into a quantum state. This process is crucial because quantum computers operate on qubits, which exist in superposition and can represent more complex information than classical bits, but require a specific method of translation. The choice of encoding significantly impacts the algorithm’s performance and efficiency.

Classical Data Encoding Methods

Several techniques exist for encoding classical data into quantum states. The most straightforward is amplitude encoding, where the classical data is directly encoded into the amplitudes of a quantum state. For example, a binary vector [0, 1] could be encoded as a qubit in the state |1⟩. Another common approach is basis encoding, where each bit of the classical data is mapped to a specific basis state of a qubit.

A binary vector [1, 0, 1] could be encoded into three qubits in the state |101⟩. These methods are relatively simple but can become inefficient for higher-dimensional data. Other techniques like angle encoding and feature map encoding are used to handle more complex data structures and improve the efficiency of quantum machine learning algorithms.

Quantum Data Encoding Techniques

Amplitude encoding directly maps classical data into the amplitudes of a quantum state. This method is efficient for low-dimensional data but suffers from exponential scaling issues for higher dimensions. Angle encoding represents data as angles in a quantum state, making it suitable for certain machine learning tasks where angular relationships are significant. For example, in classifying images, the angles representing image features can be encoded into qubits using this technique.

However, it may not be ideal for tasks requiring precise amplitude representation. Finally, feature map encoding uses a transformation function to map classical data into a higher-dimensional quantum feature space, improving the algorithm’s ability to discriminate between data points. This is particularly useful for high-dimensional data sets where linear separability is a challenge.

Challenges of High-Dimensional Data Representation

Representing high-dimensional data in a quantum context presents significant challenges. The number of qubits required grows exponentially with the dimensionality of the data. This leads to a problem known as the qubit scaling problem, which limits the applicability of quantum algorithms to high-dimensional data sets. Furthermore, efficient and effective encoding schemes for high-dimensional data are still under development. While techniques like feature map encoding aim to mitigate this issue, they can be computationally expensive and require careful selection of the transformation function.

The limited connectivity of current quantum computers also presents a challenge, as it affects the efficiency of manipulating encoded data.

Comparison of Quantum Data Encoding Methods

Encoding Method	Advantages	Disadvantages	Suitable for
Amplitude Encoding	Simple, intuitive	Scalability issues with high-dimensional data	Low-dimensional data
Angle Encoding	Efficient for angular relationships	May not capture amplitude information accurately	Tasks involving angular relationships
Basis Encoding	Simple to implement	Requires a large number of qubits for high-dimensional data	Data with binary or categorical features
Feature Map Encoding	Handles high-dimensional data, potential for improved discrimination	Computationally expensive, requires careful selection of feature map	High-dimensional data, complex datasets

Challenges and Future Directions of Quantum Machine Learning

Quantum machine learning (QML) holds immense promise, but significant hurdles remain before it can reach its full potential. The current state of the art is characterized by a gap between theoretical advancements and practical implementation, hampered by limitations in both hardware and software. Overcoming these challenges requires a multi-pronged approach, focusing on improving hardware capabilities, developing robust error mitigation techniques, and exploring innovative hybrid approaches.

Limitations of Quantum Machine Learning Hardware and Software

Current quantum computers are significantly limited in terms of qubit count, coherence times, and gate fidelity. These limitations directly impact the size and complexity of machine learning models that can be implemented. For instance, the number of qubits available restricts the dimensionality of data that can be processed effectively, limiting the applicability of QML to certain problem domains.

Furthermore, the susceptibility of qubits to noise and decoherence necessitates the development of sophisticated error correction schemes, which are currently computationally expensive and often reduce the effective number of usable qubits. Software development for QML is also in its nascent stages, lacking the maturity and user-friendliness of classical machine learning frameworks. The development of more efficient quantum algorithms and optimized software tools is crucial for accelerating the progress of the field.

For example, current quantum simulators, while helpful for testing and development, often cannot accurately reflect the behavior of real quantum hardware.

Challenges Associated with Error Correction in Quantum Computation for Machine Learning

Error correction is paramount for realizing fault-tolerant quantum computation, a prerequisite for practical QML applications. Quantum systems are inherently fragile, susceptible to errors introduced by environmental noise and imperfections in the hardware. Implementing effective error correction codes requires significant overhead in terms of qubit resources and computational complexity. This overhead further exacerbates the limitations imposed by the current hardware constraints.

Furthermore, the development of efficient error correction schemes specifically tailored for machine learning algorithms is still an active area of research. Finding a balance between the level of error correction required and the computational resources available is a key challenge. One approach involves developing new quantum error-correcting codes that are more efficient and robust to the types of noise prevalent in current quantum computers.

Potential for Hybrid Quantum-Classical Machine Learning Approaches

Given the limitations of current quantum hardware, hybrid quantum-classical approaches offer a promising pathway to near-term progress. These approaches leverage the strengths of both classical and quantum computing paradigms, combining the computational power of classical machines with the potential speedup offered by quantum algorithms for specific tasks. For example, a hybrid model might use a classical computer for preprocessing data, feature extraction, and post-processing, while employing a quantum computer to perform specific computationally intensive tasks, such as optimization or classification.

This approach allows us to explore the benefits of QML even with limited quantum resources. A successful example could be using a quantum annealer to optimize the hyperparameters of a classical neural network, thereby potentially improving its performance.

Quantum machine learning holds immense potential, but realizing that potential requires overcoming significant hurdles. A key area of research focuses on understanding the practical limitations of current approaches, as detailed in this insightful article: Exploring the limitations and challenges of current quantum AI algorithms. Overcoming these challenges is crucial for unlocking the true power of quantum machine learning and its transformative applications.

Future Research Directions Needed to Advance the Field of Quantum Machine Learning

Future research in QML should focus on several key areas. Developing more efficient quantum algorithms for machine learning tasks is crucial, potentially focusing on algorithms that are less susceptible to noise and require fewer qubits. Further advancements in quantum hardware are essential, particularly in increasing qubit coherence times and reducing error rates. This includes exploring new qubit technologies and improving fabrication techniques.

Simultaneously, the development of more robust and efficient error correction codes tailored for QML applications is paramount. Finally, exploring novel quantum data representations and encoding schemes could significantly impact the performance and efficiency of QML algorithms. Research into hybrid quantum-classical algorithms and frameworks will continue to be critical for bridging the gap between theory and practical application.

This includes developing user-friendly software tools and libraries that simplify the development and deployment of hybrid QML models.

Applications of Quantum Machine Learning

Quantum machine learning (QML) is a rapidly developing field with the potential to revolutionize various sectors by leveraging the unique capabilities of quantum computers. While still in its early stages, QML is already showing promise in tackling complex problems beyond the reach of classical computing. Its applications span diverse fields, offering solutions to computationally intensive tasks and potentially unlocking new scientific discoveries.

Drug Discovery

Quantum machine learning is poised to significantly accelerate drug discovery by improving the accuracy and efficiency of various stages in the process. For example, QML algorithms can be used to model the complex interactions between molecules and proteins, predicting binding affinities with higher accuracy than classical methods. This allows researchers to identify potential drug candidates more effectively and reduce the time and cost associated with experimental testing.

One promising application is in virtual screening, where QML can analyze vast databases of molecules to identify those most likely to bind to a specific target, significantly narrowing down the pool of candidates for further investigation. Furthermore, QML can aid in designing novel molecules with specific properties, potentially leading to the development of more effective and targeted therapies.

For instance, researchers are exploring the use of quantum algorithms to optimize the design of drug molecules, improving their efficacy and reducing side effects.

Materials Science

The discovery and design of new materials with specific properties is a computationally intensive task. Quantum machine learning offers a powerful tool to accelerate this process. QML algorithms can be used to model the electronic structure and properties of materials, predicting their behavior under different conditions. This can help researchers identify new materials with desirable characteristics, such as high strength, conductivity, or catalytic activity.

For example, QML could be used to predict the properties of novel alloys or to design new catalysts for chemical reactions. By accurately simulating the behavior of materials at the atomic level, QML can drastically reduce the time and resources required for experimental synthesis and characterization, ultimately leading to faster innovation in various industries.

Financial Modeling

The financial industry deals with massive datasets and complex models. Quantum machine learning offers the potential to improve the accuracy and efficiency of various financial tasks. For instance, QML algorithms can be used to develop more sophisticated risk management models, predicting market fluctuations and identifying potential risks more accurately than classical methods. Another application is in portfolio optimization, where QML can help investors construct portfolios that maximize returns while minimizing risk.

Furthermore, QML could improve fraud detection by identifying patterns and anomalies in financial transactions that are difficult to detect using classical methods. The ability of QML to handle high-dimensional data and complex relationships makes it particularly well-suited for these tasks. Consider, for example, a scenario where QML is used to predict the price of a specific stock based on a vast array of market indicators – its ability to analyze these complex interactions offers a potential advantage over traditional methods.

Potential Applications Across Various Industries

Quantum machine learning’s potential extends far beyond the examples mentioned above. The following list highlights some other promising areas of application:

• Artificial Intelligence: Enhancing the performance of AI algorithms, particularly in areas like image recognition and natural language processing.
• Climate Change Modeling: Developing more accurate climate models to better understand and predict the effects of climate change.
• Cybersecurity: Improving the security of systems by detecting and preventing cyberattacks more effectively.
• Optimization Problems: Solving complex optimization problems in logistics, supply chain management, and traffic flow.
• Healthcare: Improving diagnostics, personalized medicine, and drug discovery.

Illustrative Example: Quantum Machine Learning in Drug Discovery

Quantum machine learning (QML) holds immense promise for accelerating drug discovery, a notoriously time-consuming and expensive process. This example demonstrates how a variational quantum eigensolver (VQE) can be used to predict the binding affinity of a molecule to a target protein, a crucial step in identifying potential drug candidates.This process involves using a QML algorithm to model the interaction energy between a drug molecule and its target protein.

Lower interaction energies generally indicate stronger binding and thus, higher potential efficacy. We will walk through a simplified representation of this process, focusing on the core concepts.

Data Preprocessing

The first step involves representing the molecule and protein structures digitally. This typically uses techniques like graph representation, where atoms are nodes and bonds are edges, or more sophisticated methods involving 3D coordinates and electron density. These representations are then converted into a format suitable for quantum computation, often involving encoding the structural information into the qubit states of a quantum computer.

Feature selection, a critical aspect of classical machine learning, also plays a vital role here. Relevant molecular descriptors that capture crucial interaction characteristics are selected to minimize the computational burden while maintaining predictive accuracy. This could involve selecting features like atom types, bond lengths, and partial charges.

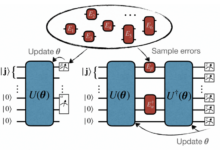
Algorithm Implementation: Variational Quantum Eigensolver (VQE)

The VQE is a hybrid quantum-classical algorithm well-suited for this task. It aims to find the ground state energy of a quantum system, which in this case represents the binding energy between the molecule and protein. The process begins by encoding the molecular features into the initial state of a set of qubits. A parameterized quantum circuit, often a variational ansatz, is then applied to these qubits, creating a superposition of states.

This ansatz is designed to explore a relevant subspace of the entire Hilbert space, reducing the computational complexity. The classical part of the algorithm involves optimizing the parameters of the quantum circuit to minimize the expectation value of the Hamiltonian representing the molecule-protein interaction. This optimization is typically done using classical optimization algorithms like gradient descent. The expectation value is estimated by measuring the qubits after the quantum circuit’s execution.

Result Analysis

After the optimization process, the VQE provides an estimate of the ground state energy, which represents the binding affinity. Lower energy values indicate stronger binding. This prediction can then be compared to experimental data or results from classical molecular dynamics simulations. The accuracy of the VQE prediction depends on factors such as the quality of the quantum circuit ansatz, the accuracy of the Hamiltonian, and the quality of the classical optimization algorithm.

The success of this approach is evaluated by comparing the predicted binding affinities with experimental data or classical simulations, using metrics such as mean absolute error (MAE) or R-squared. A high R-squared value indicates a strong correlation between predicted and experimental values, indicating a good model fit.

Illustrative Image Description

Imagine a diagram showing a data flow. On the left, we have a 3D representation of a drug molecule and its target protein. Arrows point to the right, indicating the data transformation steps. First, the 3D structures are converted into a simplified graph representation (nodes for atoms, edges for bonds). This graph then undergoes feature extraction, leading to a set of numerical features.

These features are encoded into the initial state of qubits. The qubits pass through a parameterized quantum circuit (VQE). The output of the circuit is measured, and the result is fed into a classical optimization algorithm (e.g., gradient descent). This loop continues until the energy is minimized. Finally, the minimized energy, representing the binding affinity, is outputted and compared to experimental data.

The diagram visually represents the flow from raw structural data to a predicted binding affinity.

Quantum machine learning holds incredible potential, offering speed and power beyond classical methods. However, realizing this potential requires incredibly fast data transfer, which is where Low-latency communication becomes crucial. Without near-instantaneous data exchange, the benefits of quantum algorithms are severely hampered, highlighting the vital interdependence of these two rapidly advancing fields.

Concluding Remarks

Quantum machine learning is still in its nascent stages, but its potential is undeniable. While challenges remain in terms of hardware development and error correction, the progress made thus far is remarkable. The convergence of quantum computing and machine learning promises a future where we can tackle problems previously considered unsolvable, leading to breakthroughs in diverse fields such as drug discovery, materials science, and financial modeling.

Further research and development will undoubtedly unlock even more powerful capabilities, ushering in a new era of technological advancement.

FAQ Overview: Quantum Machine Learning

What is the biggest current limitation of quantum machine learning?

The biggest limitation is the availability of stable, scalable, and fault-tolerant quantum computers. Current quantum computers are relatively small and prone to errors.

How does quantum machine learning differ from classical machine learning in terms of data processing?

Classical machine learning processes data bit by bit. Quantum machine learning leverages superposition and entanglement to process multiple data points simultaneously, potentially leading to exponential speedups for certain tasks.

Are there any ethical concerns surrounding quantum machine learning?

Yes, as with any powerful technology, ethical concerns exist. These include potential biases in algorithms, the responsible use of the technology, and ensuring equitable access to its benefits.

What programming languages are commonly used in quantum machine learning?

Several languages are used, including Python with libraries like Qiskit, Cirq, and PennyLane, which provide tools for quantum algorithm development and simulation.

When can we expect widespread practical applications of quantum machine learning?

This is difficult to predict precisely. While some niche applications are emerging, widespread practical use is likely still several years away, pending significant advancements in quantum hardware.